Back to Shell Centre papers

On Computer Based Assessment of Mathematics

Daniel Pead - August 2010

Thesis submitted to the University of Nottingham for the degree of Doctor of Philosophy

Abstract

This work explores some issues arising from the widespread use of computer based assessment of Mathematics in primary and secondary education. In particular, it considers the potential of computer based assessment for testing “process skills” and “problem solving”. This is discussed through a case study of the World Class Tests project which set out to test problem solving skills.

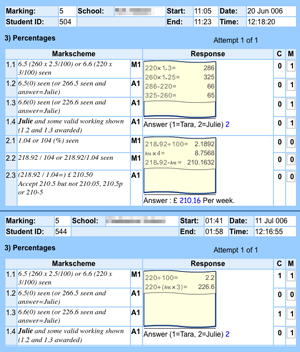
The study also considers how on-screen “eAssessment” differs from conventional paper tests and how transferring established assessment tasks to the new media might change their difficulty, or even alter what they assess. Once source of evidence is a detailed comparison of the paper and computer versions of a commercially published test – nferNelson's Progress in Maths - including a new analysis of the publisher's own equating study.

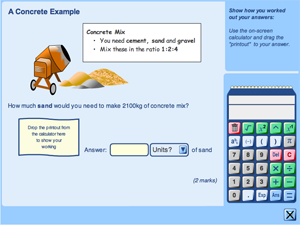
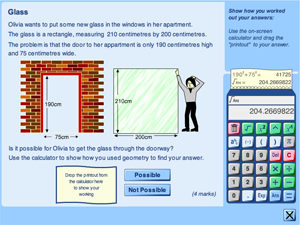
The other major aspect of the work is a design research exercise which starts by analysing tasks from Mathematics GCSE papers and proceeds to design, implement and trial a computer-based system for delivering and marking similar styles of tasks. This produces a number of insights into the design challenges of computer-based assessment, and also raises some questions about the design assumptions behind the original paper tests. One unanticipated finding was that, unlike younger pupils, some GCSE candidates expressed doubts about the idea of a computer-based examination.

The study concludes that implementing a Mathematics test on a computer involves detailed decisions requiring expertise in both assessment and software design, particularly in the case of richer tasks targeting process skills. It concludes with the proposal that, in contrast to its advantages in literacy-based subjects, the computer may not provide a “natural medium for doing mathematics”, and instead places an additional demand on students. The solution might be to reform the curriculum to better reflect the role of computing in modern Mathematics.